| The Definition of e and the Derivative of ex |
| f ' (x) = |
|
| = ax |
|
|
|
|
|
|
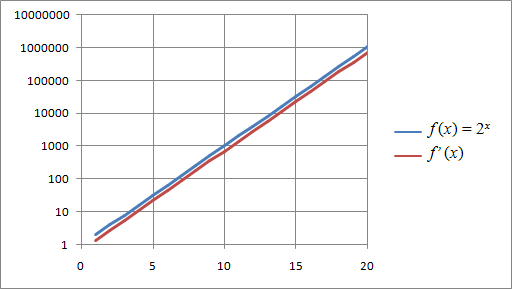
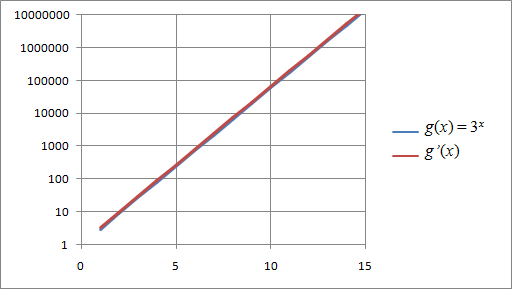
| (ax ) = ax ? |
|
| = 1 |
|
| ≈ 1 |
| h | (1 + h)1/h |
| 0.001 | 2.716923932 |
| 0.0001 | 2.718145927 |
| 0.00001 | 2.718268237 |
| 0.000001 | 2.718280469 |
| 0.0000001 | 2.718281694 |
| 0.00000001 | 2.718281798 |
| e = |
| (1 + h)1/ h = 2.718... |
|
| = 1 |
| (ex ) = ex |
| (2x ) = (ln 2)2x |
| (3x ) = (ln 3)3x |
| (ax ) = (ln a)ax |