Quick
A polynomial is an equation of the form: y = f(x) = anxn + an − 1xn − 1 + ⋅⋅⋅ + a1x + a0, where n is the degree of the polynomial. All constants a0 through an can be any number, including 0.
Details
A polynomial follows the form:
y = f(x) = anxn + an − 1xn − 1 + ⋅⋅⋅ + a1x + a0
where n is a positive integer called the degree of the polynomial, and an, an − 1 , . . . , a1, a0 are constants, with leading coefficient an ≠ 0. An example of a polynomial of degree n = 3 is:
y = f(x) = 3x3 − 5x2 − x − 8
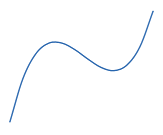
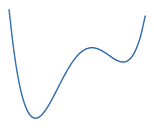
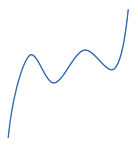
In this case a3 = 3, a2 = –5, a1 = –1, and a0 = –8. The shape of the graph of a polynomial depends on its degree. Typical graphs are shown below for degrees 2 to 5:

|  |  |  |
Quadratic
n = 2 | Cubic
n = 3 | Quantic
n = 4 | Quintic
n = 5 |
These graphs correspond to a positive coefficient for xn ; a negative coefficient turns the graph upside down. Notice the graph of the quadratic "bends" once, the cubic "bends" twice, and the quartic "bends" three times. An nth degree polynomial "bends" at most n − 1 times (where n is a positive integer), but there may be fewer turns.
Some of the best known functions for which there are formulas are polynomials:
Related
▪ L - Taylor Polynomials







