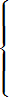---

Complex Numbers, Real and Imaginary

---

Quick
complex number - A complex number is defined as any number that includes both real numbers and imaginary numbers.
real number - A real number may be either rational or irrational; either algebraic or transcendental; and either positive, negative, or zero.
imaginary number - An imaginary number is a real number multiplied by i, where i is the imaginary unit.


Equations

(Eq1)     i2 = –1	equation for the imaginary number i
(Eq2)     z = a + bi	equation for complex number

Nomenclature

a	real number
b	real number
i	√  −1   , the imaginary unit
z	complex number

Rules for Manipulating Complex Numbers

(a + bi) + (c + di) = (a + c) + (b + d)i	Adding two complex numbers is done by adding real and imaginary parts separately
(a + bi) − (c + di) = (a − c) + (b − d)	Subtracting two complex numbers is done by subtracting real and imaginary parts separately
(a + bi)(c + di) = a(c + di) + bi(c + di) = = ac + adi + bci + bdi2 = ac + adi + bci − bd = (ac − bd) + (ad + bc)i	Multiplication works just like for polynomicals, using i2 = −1
(bi)n = bnin = 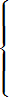bni     for n = 1, 5, 9, 13,... −bn     for n = 2, 6, 10, 14,... −bni     for n = 3, 7, 11, 15,... bn     for n = 4, 8, 12, 16,...	Powers of i: It is known that i2 = −1; then i3 = (i)(i2) = −i, and i4 = (i2)2 = (−1)2 = 1. Then i5 = (i)(i4) = i, and so on.
(z)( z ) = (a + bi)(a − bi) = a2 − abi + abi − b2i2 = a2 + b2	The product of a number and its conjugate is always real and nonnegative.
a + bi c + di  =  ( a + bi c + di )( c − di c − di )  =  ac − adi + bci − bdi2 c2 − d2  =  ac + bd c2 + d2  +  bc − ad c2 + d2 i	Dividing is done by multiplying the denominator by its conjugate, thereby making the denominator real.

Details

The quadratic equation:

x² − 2x + 2 = 0

is not satisfied by any real number x. In applying the quadratic formala, the following results:

x =

2 ± √  4 − 8  2

= 1 ±

√  −4  2

Apparently, the square root of −4 must be taken. But −4 doesn't have a square root, at least, not one which is a real number. Therefore, it is given a square root in the following manner. An imaginary number i is defined such that:

(Eq1)

i2 = –1

With this i:

(2i)² = 4i ² = −4

so:

x = 1 ±

√  −4  2

= 1 ±

2i 2

= 1 ± i

This solves the quadratic equation. The numbers 1 + i and 1 − i are examples of complex numbers.

A complex number is defined as any number that can be written in the form:

(Eq2)

z = a + bi

The real part of z is a and the imaginary part of z is bi.

Calling the number i makes it sound as if i doesn't exist in the same way that real numbers exist. In some cases, it is useful to make such a distinction between real and imaginary numbers. For example, if mass or position are measured, the answers should be real numbers. But the imaginary numbers are just as legitimate mathematically as real numbers.

As an analogy, consider the distinction between positive and negative numbers. Originally, people thought of numbers only as tools to count with; their concept of "five" or "ten" was not far removed from "five arrows" or "ten stones." They were unaware that negative numbers existed at all. When negative numbers were introduced, they were viewed only as a device for solving equations like x + 2 - 1. The were considered "non-numbers," or, in Latin, "negative numbers." Thus, even though people started to use negative numbers, ehty did not view them as existing in the same way that positive numbers did. An early mathematician might have reasoned: "The number 5 exists because I can have 5 coins in my hand. But how can I have −5 coins in my hand?" The answer is "I have −5 coins" means that 5 coins are owed. Negative numbers are just as real as positive ones, and that in some cases, negative numbers can have physical meaning, even though they are useless for measuring length or keeping baseball scores. Complex numbers can have physical meaning as well. For example, complex numbers are used in studying wave motion in electric circuits.

Numbers such as 0, 1, ½, π, and

√

2

are called purely real because they contain no imaginary components. Numbers such as i, 2i, and

√

2

i are called purely imaginary because they contain only the number i multiplied by a nonzero real coefficient.

Two complex numbers are called conjugates if their real parts are equal and if their imaginary parts are opposites. The complex conjugate of the complex number:

z = a + bi

is denoted by

z

(pronounced "z bar"), so:

z

= a − bi

(Note that z is real if and only if z =

z

.) Complex conjugates have the following property: if f (x) is any polynomial with real coefficients (x³ + 1, say) and f (z) = 0, then f (

z

) = 0. This means that if z is the solution to a polynomial equation with real coefficients, then so is

z

.