---

Radians and Circles

---

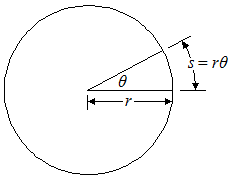
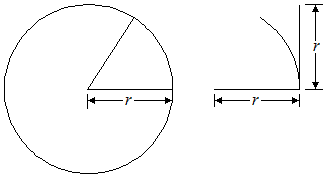
In describing rotational motion, the most natural way to measure the angle θ is not in degrees, but in radians. As shown in the figure, one radian (1 rad) is the angle subtended at the center of a circle by an arc with a length equal to the radius of the circle. In the figure, an angle θ is subtended by an arc of length s on a circle of radius r.	If the arc length s is flattened, it would measure as the same linear length as r.
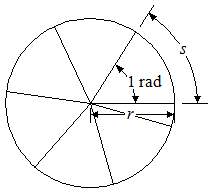
There are 2π, or about 6.283, radians in one revolution of a circle.

The value of θ (in radians) is equal to s divided by r:

(Eq1)

θ = s r

or:

s = rθ

An angle in radians is the ratio of two lengths, so it is a pure number, without dimensions. If s = 3.0 m and r = 2.0 m, then θ = 1.5, but this value will often be written as 1.5 rad to distinguish it from an angle measured in degrees or revolutions.

The circumference of a circle (that is, the arc length all the way around the circle) is 2π times the radius, so there are 2π (about 6.283) radians in one complete revolution (360°). Therefore:

1 rad =

360° 2π

= 57.296°

Similarly, 180° = π, 90° = π/2 rad, and so on. If the angle θ is measured in degrees, then a factor of (2π/360) would have to be added on the right-hand side of Eq1. By measuring angles in radians, the relationship between angle and distance along an arc is kept as simple as possible.