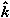This lesson will cover the acceleration of a particle moving in space. Just as for motion in a straight line, acceleration describes how the velocity of the particle changes. But now, acceleration will be generalized to describe changes in the magnitude of the velocity (that is, the speed) and changes in the direction of the velocity (that is, the direction in which the particle is moving in space).
In the following figures, a particle is moving along a curved path. The vectors  1 and
1 and  2 represent the particle's instantaneous velocities at time t1, when the particle is at point P1, and at time t2, when the particle is at point P2. The two velocities may differ in both magnitude and direction. The average acceleration
2 represent the particle's instantaneous velocities at time t1, when the particle is at point P1, and at time t2, when the particle is at point P2. The two velocities may differ in both magnitude and direction. The average acceleration 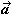 av of the particle as it moves from P1 to P2 as the vector change in velocity,
av of the particle as it moves from P1 to P2 as the vector change in velocity,  2 −
2 −  1 = Δ
1 = Δ , divided by the time interval t2 − t1 = Δt:
, divided by the time interval t2 − t1 = Δt:
Average acceleration is a vector quantity in the same direction as the vector Δ . Note that
. Note that  2 is the vector sum of the original velocity
2 is the vector sum of the original velocity  1 and the change Δ
1 and the change Δ .
.
As with the lesson in velocity and acceleration, the instantaneous acceleration a at point P1 as the limit approached by the average acceleration when point P2 approaches point P1 and Δ and Δt both approach zero; the instantaneous acceleration is also equal to the instantaneous rate of change of velocity with time. Because restriction is not limited to straight-line motion, instantaneous acceleration is now a vector:
and Δt both approach zero; the instantaneous acceleration is also equal to the instantaneous rate of change of velocity with time. Because restriction is not limited to straight-line motion, instantaneous acceleration is now a vector:
The velocity vector  , as has been observed, is tangent to the path of the particle. But the construction in the figure shows that the instantaneous acceleration vector
, as has been observed, is tangent to the path of the particle. But the construction in the figure shows that the instantaneous acceleration vector 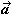 of a moving particle always points toward the concave side of a curved path — that is, toward the inside of any turn that the particle is making. It can also be observed that when a particle is moving in a curved path, it always has nonzero acceleration, even when it moves with constant speed. This conclusion may seem contrary to your intuition, but it's really just contrary to the veryday use of the word "acceleration" to mean that speed is increasing. The more precise definition given in Eq1 shows that there is a nonzero acceleration whenever the velocity vector changes in any way, whether there is a change of speed, direction, or both.
of a moving particle always points toward the concave side of a curved path — that is, toward the inside of any turn that the particle is making. It can also be observed that when a particle is moving in a curved path, it always has nonzero acceleration, even when it moves with constant speed. This conclusion may seem contrary to your intuition, but it's really just contrary to the veryday use of the word "acceleration" to mean that speed is increasing. The more precise definition given in Eq1 shows that there is a nonzero acceleration whenever the velocity vector changes in any way, whether there is a change of speed, direction, or both.
To be convinced that a particle has nonzero acceleration when moving on a curved path with constant speed, think of sensations when riding in a car. When the car accelerates, one tends to move within the car in a direction opposite to the car's acceleration. Thus one tends to slide toward the back of the car when it accelerates forward (speeds up) and toward the front of the car when it accelerates backward (slows down). If the car makes a turn on a level road, one tends to slide toward the outside of the turn; hence the car has an acceleration toward the inside of the turn.
Interest usually lies with instantaneous acceleration, in contrast to average acceleration. Typically when the word acceleration is used, it is with reference to instantaneous acceleration. Each component of the acceleration vector is the derivative of the corresponding componenet of velocity:
These equations are the components of instantaneous acceleration. They may also be represented in terms of unit vectors:
Because each component of velocity is the derivative of the corresponding coordinate, the components ax, ay, and az of the acceleration vector,  , as:
, as:
And then the acceleration vector may be expressed as:
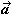 =
= 2 −
2 −  1
1
 1 and
1 and  2 represent the particle's instantaneous velocities at time t1, when the particle is at point P1, and at time t2, when the particle is at point P2. The two velocities may differ in both magnitude and direction. The average acceleration
2 represent the particle's instantaneous velocities at time t1, when the particle is at point P1, and at time t2, when the particle is at point P2. The two velocities may differ in both magnitude and direction. The average acceleration 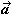 av of the particle as it moves from P1 to P2 as the vector change in velocity,
av of the particle as it moves from P1 to P2 as the vector change in velocity,  2 −
2 −  1 = Δ
1 = Δ , divided by the time interval t2 − t1 = Δt:
, divided by the time interval t2 − t1 = Δt:
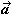 =
= . Note that
. Note that  2 is the vector sum of the original velocity
2 is the vector sum of the original velocity  1 and the change Δ
1 and the change Δ .
.
 and Δt both approach zero; the instantaneous acceleration is also equal to the instantaneous rate of change of velocity with time. Because restriction is not limited to straight-line motion, instantaneous acceleration is now a vector:
and Δt both approach zero; the instantaneous acceleration is also equal to the instantaneous rate of change of velocity with time. Because restriction is not limited to straight-line motion, instantaneous acceleration is now a vector:
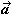 =
=  , as has been observed, is tangent to the path of the particle. But the construction in the figure shows that the instantaneous acceleration vector
, as has been observed, is tangent to the path of the particle. But the construction in the figure shows that the instantaneous acceleration vector 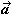 of a moving particle always points toward the concave side of a curved path — that is, toward the inside of any turn that the particle is making. It can also be observed that when a particle is moving in a curved path, it always has nonzero acceleration, even when it moves with constant speed. This conclusion may seem contrary to your intuition, but it's really just contrary to the veryday use of the word "acceleration" to mean that speed is increasing. The more precise definition given in Eq1 shows that there is a nonzero acceleration whenever the velocity vector changes in any way, whether there is a change of speed, direction, or both.
of a moving particle always points toward the concave side of a curved path — that is, toward the inside of any turn that the particle is making. It can also be observed that when a particle is moving in a curved path, it always has nonzero acceleration, even when it moves with constant speed. This conclusion may seem contrary to your intuition, but it's really just contrary to the veryday use of the word "acceleration" to mean that speed is increasing. The more precise definition given in Eq1 shows that there is a nonzero acceleration whenever the velocity vector changes in any way, whether there is a change of speed, direction, or both.
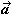 =
=  +
+ 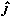 +
+ 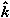
 , as:
, as:
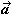 =
=  +
+ 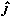 +
+