Conduction Shape Factors

In cases 1 through 8 and case 11, two-dimensional conduction is presumed to occur between the boundaries that are maintained at uniform temperatures, with ΔT1−2 = T1 − T2. In case 9, three-dimensional conduction exists in the corner region, while in case 10, conduction occurs between an isothermal disk (T1) and a semi-infinite medium of uniform temperature (T2) at locations well removed from the disk. Shape factors may also be defined for one-dimensional geometries as given by cases 12 through 14.

q = Sk(T1 − T2)
System Schematic Restrictions Shape Factor
Case 1
Isothermal sphere buried in a semi-infinite medium		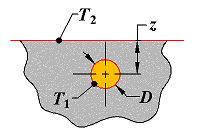 z > D/2
2πD
1 − D/4z
Case 2
Horizontal isothermal cylinder of length L buried in a semi-infinite medium
L >> D

L >> D
z > 3D/2
2πL
cosh–1 (2z/D)
2πL
ln (4z/D)
Case 3
Vertical cylinder in a semi-infinite medium		 L >> D
2πL
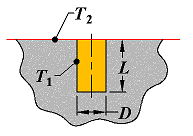ln (4L/D)
Case 4
Conduction between two cylinders of length L in infinite medium		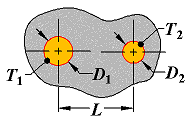 L >> D1, D2
L >> w
2πL
cosh−1 (
4w2 − D12 − D22
2D1D2
 )
Case 5
Horizontal circular cylinder of length L midway between parallel planes of equal length and infinite width		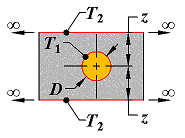 z >> D/2
L >> z
2πL
ln (8z/πD)
Case 6
Circular cylinder of length L centered in a square solid of equal length		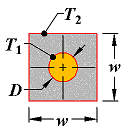 w > D
L >> w
2πL
ln (1.08w/D)
Case 7
Eccentric circular cylinder of length L in a cylinder of equal length		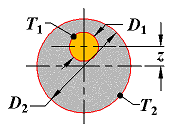 D2 > D1
L >> D2
2πL
cosh−1 (
D22 + D12 − 4z2
2D1D2
 )
Case 8
Conduction through the edge of adjoining walls		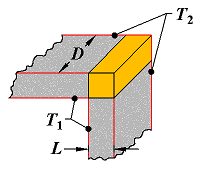 D > 5L 0.54D
Case 9
Conduction through corner of three walls with a temperature difference ΔT1−2 across the walls		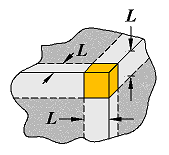 L << length and width of wall 0.15L
Case 10
Disk of diameter D and temperature T1 on a semi-infinite medium of thermal conductivity k and temperature T2		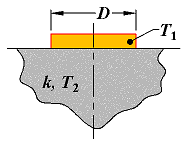 None 2D
Case 11
Square channel of length L		 w2/w1 < 1.4

w2/w1 > 1.4
L >> w2
2πL
0.785 ln (w2/w1)


2πL
0.930 ln (w2/w1) − 0.050
Case 12
One-dimensional heat transfer through plane wall		    
A
L
Case 13
One-dimensional heat transfer through cylindrical wall		    
2πL
ln(r2/r1)
Case 14
One-dimensional heat transfer through spherical wall		    
4πr1r2
(r2 − r1)