---

Viscosity and Flow Between Plates

---

symbol	description
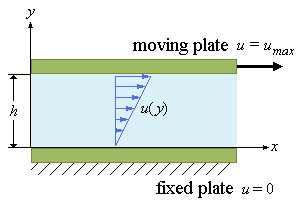
u	velocity of fluid along the velocity profile
umax	velocity at the moving wall
h	distance between top and bottom plates
τ	shear stress
μ	viscosity
C	a constant

A problem of interest is the flow induced between a lower plate that is fixed and an upper plate moving with a constant velocity u_max as shown in the figure below.



The fluid does not slip slip at either plate. If the plates are large, this steadily shearing motion will result in a velocity distribution u( y). The fluid acceleration is zero everywhere.

With zero acceleration and assuming no pressure variation in the flow direction, a force balance on a small fluid element leads to the result that the shear stress is constant thoughout the fluid:

du dy

=

τ μ

=  C

Fluids that obey the above relation are considered Newtonian fluids. From the above,

du = Cdy

which can be integrated to get:

u = C₁ + C₂ y

evaluating C₁ and C₂ from the conditions at each wall:

u =

{

0 = C1 + C2(0) umax = C1 + C2(h)

Therefore, C1 = 0 and C2 =

umax h

Then the velocity profile between the plates is given by:

u( y)  =

y h

umax

So if y equals h, then u(y) = u_max.

Because of the relation:

du dy

=

umax h

The following equation may result:

τ =  μ

umax h

Typically, viscosity stresses have a small impact on fluid motion.