| Conservation of Energy for a Control Volume |
The subjects of thermodynamics and heat transfer are highly complementary. For example, because it treats the rate at which heat is transferred, the subject of heat transfer may be viewed as an extension of thermodynamics. Conversely, for many heat transfer problems, the first law of thermodynamics (the law of conservation of energy) provides a useful, often essential, tool. In anticipation of such problems, general formulations of the first law are obtained.
At its heart, the first law of thermodynamics is simply a statement that the total energy of a system is conserved, and therefore the only way that the amount of energy in a system can change is if energy crosses its boundaries. The first law also addresses the ways in which energy can cross the boundaries of a system. For a closed system (a region of fixed mass), there are only two: heat transfer through the boundaries and work done on or by the system. This leads to the following statement of the first law for a closed system:
where ΔEsttot is the change in the total energy stored in the system, Q is the net heat transferred to the system, and W is the net work done by the system. This is schematically illustrated below:
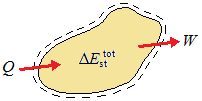 | conservation of energy for a closed system over a time interval |
The first law can also be applied to a control volume (or open system), a region of space bounded by a control surface through which mass may pass. Mass entering and leaving the control volume carries energy with it; this process, termed energy advection, adds a third way in which energy can cross the boundaries of a control volume. To summarize, the first law of thermodynamics can be very simply states as follows for both a control volume and a closed system.
First Law of Thermodynamics over a Time Interval (Δt)
The increase in the amount of energy stored in a control volume must equal the amount of energy that enters the control volume, minus the amount of energy that leaves the control volume.
In applying this principle, it is recognized that energy can enter and leave the control volume due to heat transfer through the boundaries, work done on or by the control volume, and energy advection.
The first law of thermodynamics addresses total energy, which consists of kinetic and potential energies (together known as mechanical energy) and internal energy. Internal energy can be further subdivided into thermal energy and other forms of internal energy such as chemical and nuclear energy. For the study of heat transfer, it is desired to focus attention on the thermal and mechanical forms of energy. We must recognize that the sum of thermal and mechanical energy is not conserved, because there can be conversion between other forms of energy and thermal energy. For example, if a chemical reaction occurs that decreases the amount of chemical energy in the system, it will result in an increase in the thermal energy of the system. Thus, energy conversion can be thought of as resulting in thermal energy generation (which can be either positive or negative). So, a statement of the first law that is well suited for heat transfer analysis is:
Thermal and Mechanical Energy Equation over a Time Interval (Δt)
The increase in the amount of thermal and mechanical energy stored in the control volume must equal the amount of thermal and mechanical energy that enters the control volume, minus the amount of thermal and mechanical energy that leaves the control volume, plus the amount of thermal energy that is generated within the control volume.
Let E stand for the sum of thermal and mechanical energy (in contrast to the symbol Etot for total energy). Using the subscript st to denote the energy stored in the control volume, the change in thermal and mechanical energy stored over the time interval Δt is then ΔEst. The subscripts in and out refer to energy entering and leaving the control volume. Finally, thermal energy generation is given the symbol Eg. Thus, the first statement can be written as:
This expression applies over a time interval Δt, and all the energy terms are measured in joules. Since the first law must be satisfied at each and every instant of time, t, the law can also be formulated on a rate basis. That is, at any instant, there must be a balance between all energy rates, as measured in joules per second (W). In words, this is expressed as:
Thermal and Mechanical Energy Equation at an Instant (t)
The rate of increase of thermal and mechanical energy stored in the control volume must equal the rate at which thermal and mechanical energy enter the control volume, minus the rate at which thermal and mechanical energy leave the control volume, plus the rate at which thermal energy is generated within the control volume.
or:
This expression is illustrated schematically below.
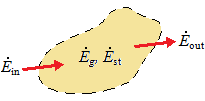 | conservation of energy for a control volume at an instant |
If the inflow and generation of thermal and mechanical energy exceed the outflow, there must be an increase in the amount of thermal and mechanical energy stored (accumulated) in the control volume; if the converse is true, there will be a decrease in thermal and mechanical energy storage. If the inflow and generation equal the outflow, a steady-state condition must prevail such that there will be no change in the amount of thermal and mechanical energy stored in the control volume.
Eq2 and Eq3 provide important and, in some cases, essential tools for solving heat transfer problems. Every application of the first law must begin with the identification of an appropriate control volume and its control surface, to which an analysis is subsequently applied. The first step is to indicate the control surface by drawing a dashed line. The second step is to decide whether to perform the analysis for a time interval Δt (Eq2) or on a rate basis (Eq3). This choice depends on the objective of the solution and the way in which information is given in the problem. The next step is to identify the energy terms that are relevant in the problem. To develop confidence in taking this last step, the remainder of this section is devoted to clarifying the following energy terms:
• stored thermal and mechanical energy, Est
• thermal energy generation, Eg
• thermal and mechanical energy transport across the control surfaces, that is, the inflow and outflow terms, Ein and Eout
In the statement of the first law (Eq1), the total energy, Etot, consists of kinetic energy, potential energy, and internal energy. Mechanical energy is defined as the sum of kinetic and potential energy. It will most often be the case in heat transfer problems that the changes in kinetic and potential energy are small and can be neglected. The internal energy consists of:
1. a sensible component, which accounts for the translational, rotational, and/or vibrational motion of the atoms/molecules comprising the matter
2. a latent component, which relates to intermolecular forces influencing phase change between solid, liquid, and vapor states
3. a chemical component, which accounts for energy stored in the chemical bonds between atoms; and
4. a nuclear component, which accounts for the binding forces in the nucleus.
For the study of heat transfer, attention is focused on the sensible and latent components of the internal energy (Usens and Ulat, respectively), which are together referred to as thermal energy, Ut. The sensible energy is the portion that is associate mainly with changes in temperature (although it can also depend on pressure). The latent energy is the component that is associated with changes in phase. For example, if the material in the control volume changes from solid to liquid (melting) or from liquid to vapor (vaporization, evaporation, boiling), the latent energy increases. Conversely, if the phase change is from vapor to liquid (condensation) or from liquid to solid (solidification, freezing), the latent energy decreases. Obviously, if there is no phase change occuring, there is no change in latent energy, and this term can be neglected.
Based on the above discussion, the stored thermal and mechanical energy is given by Est = KE + PE + Ut, where Ut = Usens + Ulat. In many problems, the only relevant energy term will be the sensible energy, that is, Est = Usens.
The energy generation term is associated with conversion from some other form of internal energy (chemical, electrical, electromagnetic, or nuclear) to thermal energy. It is a volumetric phenomenon. That is, it occurs within the control volume and is generally proportional to the magnitude of this volume. For example, an exothermic chemical reaction may be occurring, converting chemical energy to thermal energy. The net effect is an increase in the thermal energy of the matter within the control volume. Another source of thermal energy is the conversion from electrical energy that occurs due to resistance heating when an electric current is passed through a conductor. That is, if an electric currrent I passes through a resistance R in the control volume, electrical energy is dissipated at a rate I2R, which corresponds to the rate at which thermal energy is generated (released) within the volume. Usually in heat transfer applications, if chemical, electrical, or nuclear effects exist, they are treated as sources (or sinks, which correspond to negative sources) of thermal energy and hence are included in the generation terms of Eq2 and Eq3.


