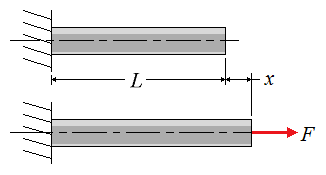
| (Eq1) | W = Fx |
| (Eq2) |
|
| (Eq3) | W = Fx cosθ =  ⋅ ⋅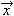 = Fx (for θ = 90°) = Fx (for θ = 90°) |
| Work |
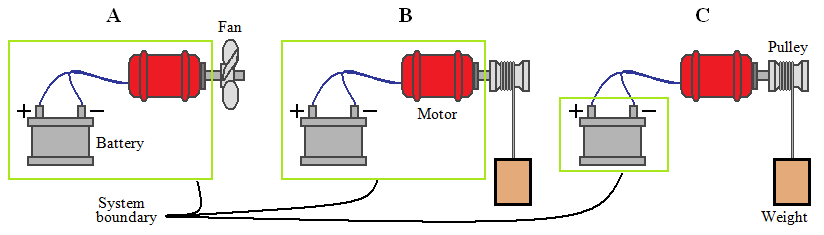
| Work defining a force acting through a distance | |||||||||
| Work expressed as an integral | |||||||||
| - |
| symbol | description |
| W | work |
| F | force (a vector quantity) |
| x | displacement (a vector quantity) |
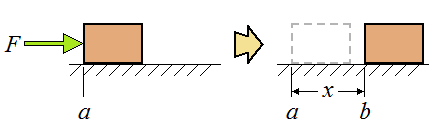
| W = Fx | 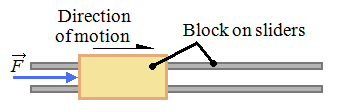 |
W = Fx cosθ =  ⋅ ⋅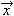 |  |
| work is positive (+) | force contributes to direction of movement | 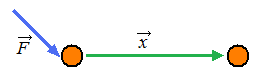 |
| work is negative (−) | force acts against direction of movement | 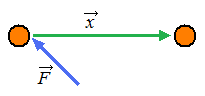 |
| work is zero, W = 0 | force has no contribution to movement | 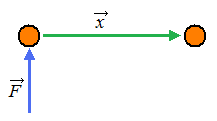 |
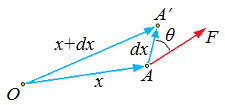
| (Eq2) |
|