Heat Versus Work

There are many similarities between heat and work:
1. Heat and work are both transient phenomena. Systems never possess heat or work, but either or both cross the system boundary when a system undergoes a change of state.
2. Both heat and work are boundary phenomena. Both are observed only at the boundaries of the system, and both represent energy crossing the boundary of the system.
3. Both heat and work are path functions and inexact differentials.

Typically, regarding sign convention, +Q represents heat transferred to the system and thus is energy added to the system, and +W represents work done by the system and thus represents energy leaving the system.

An illustration may assist in explaining the difference between heat and work. The figures show a gas contained in a rigid vessel. Resistance coils are wound around the outside of the vessel. When current flows through the resistance coils, the temperature of the gas increases.


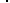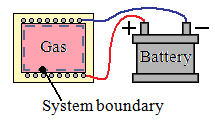
Only the gas is considered as the system. The energy crosses the boundary of the system because the temperature of the walls is higher than the temperature of the gas. Therefore, heat crosses the boundary of the system.

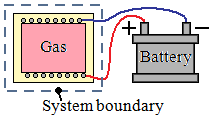
Here, the system includes the vessel and the resistance heater. Electricity crosses the boundary of the system, this is work.

Consider a gas in a cylinder fitted with a movable piston, as shown:



There is a positive heat transfer to the gas, which tends to make the temperature increase. It also tends to increase the gas pressure. However, the pressure is dictated by the external force acting on its movable boundary as discussed in the lesson Pressure. If this remains constant, then the volume increases instead. There are also the opposite tendencies for a negative heat transfer, that is, heat transfer out of the gas. Consider again the positive heat transfer, except that in this case the external force simultaneously decreases. This causes the gas pressure to decrease, such that the temperature tends to go down. In this case, there are simultaneous tendencies for temperature change in the opposite direction, which effectively decouples directions of heat transfer and temperature change.

Often, when it is desired to evaluate a finite amount of energy transferred as either work or heat, the instantaneous rate over time must be integrated:

1W 2 = ∫
2
 
1

W
dt

and:

1Q 2 = ∫
2
 
1

Q
dt

1Q2 is the heat transferred during the given process between states 1 and 2. The rate at which heat is transferred to a system is designated by the symbol

Q
:

In order to perform the integration it must be known how the rate varies with time. For time periods where the rate does not change significantly, a simple average may be of sufficient accuracy to allow the following:

1W 2 = ∫
2
 
1

W
dt		 = 

W
avg Δt

which is similar to the information given on the electricity bill as kilowatt-hours.