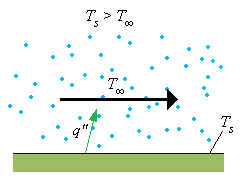
Ts is temperature at surface
T∞ is temperature of moving fluid
q" is the heat transfer from the solid surface to the moving fluid.
The difference in temperatures result in the temperature gradient.
| Convection |
| Newton's law of cooling |
| q" | convective heat flux |
| h | convection heat transfer coefficient |
| Ts | temperature at surface |
| T∞ | temperature of moving fluid |
 |
The stationary medium may be a fluid or solid
Ts is temperature at surface T∞ is temperature of moving fluid q" is the heat transfer from the solid surface to the moving fluid. The difference in temperatures result in the temperature gradient. |
| (Eq1) |
|
| h [W/mK2] | h [W/mK2] | |
| Natural convection | 5 to 25 for gas | 50 to 1000 for liquid |
| Forced convection | 25 to 250 for gas | 50 to 20000 for liquid |
| Boiling phase change | 2500 to 100000 |