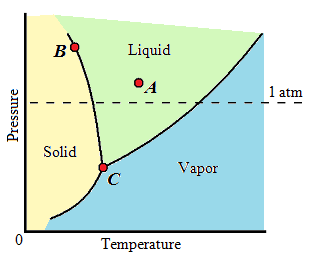
Gibbs Phase Rule

Quick
The Gibbs phase rule describes the state of a material.


Equation
F = C − P + 2 Gibbs Phase Rule


Nomenclature
Fnumber of degrees of freedom, or the amount of variables, such as temperature, pressure, or composition, that are allowed to change independently without changing the number of phases in equilibrium
Cnumber of components, usually elements or compounds, in the system
Pnumber of phases present


Details

The number 2 in the equation accounts for both temperature and pressure, and implies that they are allowed to change, that is, they are considered degrees of freedom.

Consider a hypothetical component for the following unary phase diagram in which the lines divide the solid, liquid, and vapor phases. Depending on the temperature and pressure, there may be one, two, or even three phases present at any one time. Note that the intersection of the dashed line and the solid lines, indicate the melting and boiling temperatures at atmospheric pressure. At very low pressures the solid can sublime.



Point A
Point A in the phase diagram is all liquid, and the number of components C is one and the number of phases P is one. The phase rule gives:

F = C − P + 2 = 1 − 1 + 2 = 2

There are two degrees of freedom. This imiplies that within limits, the pressure and temperature can be changed independently or together, and point A will still be in an all-liquid portion of the diagram. Put another way, the temperature and pressure must both be fixed to know precisely the conditions in the liquid portion of the diagram.

Point B
Point B is at the boundary between the solid and liquid portions of the diagram. The number of components C is still one, but at point B the solid and liquid coexist, and the number of phases P is two. From the phase rule,

F = C − P + 2 = 1 − 2 + 2 = 1

There is only one degree of freedom. So, if the temperature is changed, the pressure must also be adjusted in order to remain on the boundary where the liquid and solid coexist. On the other hand, if the pressure is fixed, the phase diagram can indicate the required temperature in order for solid and liquid to coexist.

Point C
At point C, solid, liquid, and vapor coexist. While the number of components is still one, there are three phases. The number of degrees of freedom is then:

F = C − P + 2 = 1 − 3 + 2 = 0

There are zero degrees of freedom; all three phases coexist only if both the temperature and the pressure are fixed. This is the triple point.