| Radius of Gyration of an Area |
| radius of gyration of an area with respect to the x-axis | ||||||||
| radius of gyration of an area with respect to the y-axis | ||||||||
| radius of gyration of an area about the origin | ||||||||
| equation relating radii of gyration |
| Ix | moment of inertia with respect to the x-axis |
| Iy | moment of inertia with respect to the y-axis |
| JO | polar moment of inertia |
| A | area |

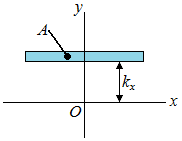
| (Eq1) |
|
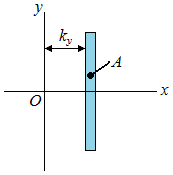
| (Eq2) |
|
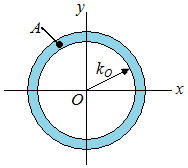
| (Eq3) |
|
| (Eq4) |
|