| Polar Moment of Inertia |
| polar moment of inertia of the area A with respect to the "pole" O | ||||||
| polar moment of inertia of a given area from the rectangular moments of inertia Ix and Iy of the area |
| r | distance from O to the element of area dA |
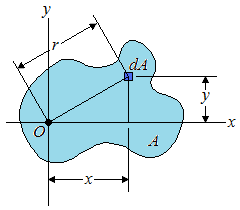
| (Eq1) |
|
| JO = | ∫ | r 2 dA = | ∫ | (x 2 + y 2) dA = | ∫ | y 2 dA + | ∫ | x 2 dA |
| (Eq2) |
|