| First Law of Thermodynamics for a Change in State of a Control Mass |
Equation
| (Eq7) | | U2 − U1 + | | + mg(Z2 − Z1) = 1Q2 − 1W2 |
|
|
first law of thermodynamics, most used form in real applications
|
Nomenclature
Details
Eq2 from the lesson First Law of Thermodynamics for a Change in State of a Control Mass states the first law of thermodynamics for a control mass during a cycle. Many times, however, the concern lies with a process rather than a cycle. A new property, the energy, is introduced and is given by the symbol E. Consider a system that undergoes a cycle in which it changes from state 1 to state 2 by process A and returns from state 2 to state 1 by process B. This cycle is shown in the pressure (or other intensive property)–volume (or other extensive property) diagram:
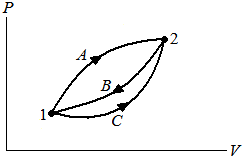
From the basic statement of the first law of thermodynamics:
Considering two separate processes:
| ∫ | | δQA + | ∫ | | δQB = | ∫ | | δWA + | ∫ | | δWB |
Now consider another cycle in which the control mass changes from state 1 to state 2 by process C and returns to state 1 by process B, as before. For this cycle:
| ∫ | | δQC + | ∫ | | δQB = | ∫ | | δWC + | ∫ | | δWB |
Subtracting the second of these equations from the first:
| ∫ | | δQA − | ∫ | | δQC = | ∫ | | δWA − | ∫ | | δWC |
rearranging:
| (Eq1) | | ∫ | | (δQ − δW)A = | ∫ | | (δQ − δW)C |
|
Since A and C represent arbitrary processes between states 1 and 2, the quantity δQ − δW is the same for all processes between states 1 and 2. Therefore, δQ − δW depends only on the initial and final states and not on the path followed between the two states. It is concluded that this is a point function, and therefore it is the differential of a property of the mass. This property is the energy of the mass and is given the symbol E. Thus it can be written:
Because E is a property, its derivative is written dE. When Eq2 is integrated from an initial state 1 to a final state 2, then:
| (Eq3) | E2 − E1 = 1Q2 − 1W2 |
where E1 and E2 are the initial and final values of the energy E of the control mass, 1Q2 is the heat transferred to the control mass during the process from state 1 to state 2, and 1W2 is the work done by the control mass during the process.
Note that a control mass may be made up of several different subsystems, as shown in the figure. In this case, each part must be analyzed and included separately in applying the first law, Eq3. It is further noted that Eq3 is an expression of the general form:
Δ Energy = + in − out
in terms of the standard sign conventions for heat and work.
The physical significance of the property E is that it represents all the energy of the system in the given state. This energy might be present in a variety of forms, such as the system of potential energy of the system as a whole with respect to the chosen coordinate frame, energy associated with the motion and position of the molecules, energy associated with the structure of the atom, chemical energy present in a storage battery, energy present in a charged condenser, or any number of other forms.
In the study of thermodynamics, it is convenient to consider bulk kinetic and potential energy separately and then to consider all the other energy of the control mass in a single property called the internal energy and which has the symbol U. Thus, it can be written:
E = internal energy + kinetic energy + potential energy
or:
E = U + EK + EP
The kinetic and potential energy of the control mass are associated with the coordinate frame that was selected and can be specified by the macroscopic parameters of mass, velocity, and elevation. The internal energy U includes all other forms of energy of the control mass and is associated with the thermodynamic state of the system.
Since the terms comprising E are point functions:
| (Eq4) | dE = dU + d(EK) + d(EP) |
The first law of thermodynamics for a change of state may therefore be written:
| (Eq5) | dE = dU + d(EK) + d(EP) = δQ − δW |
In words this equation states that as a control mass undergoes a change of state, energy may cross the boundary as either heat or work, and each may be positive or negative. The net change in the energy of the system will be exactly equal to the net energy that crosses the boundary of the system. The energy of the system may change in any of three ways—by a change in internal energy, in kinetic energy, or in potential energy.
Now, substituting the expressions Eq1 for kinetic energy and Eq1 for potential energy into Eq4:
dE = dU + mu du + mg dZ
Integrating for a change of state from state 1 to state 2 with constant g:
| E2 − E1 = U2 − U1 + | | − | | + mgZ2 − mgZ1 |
Similarly, substituting these expressions for kinetic and potential energy into Eq5:
| (Eq6) | | dE = dU + | | + d(mgZ) = δQ − δW |
|
Assuming g is a constant, in the integrated form of this equation:
| (Eq7) | | U2 − U1 + | | + mg(Z2 − Z1) = 1Q2 − 1W2 |
|
Three observations should be made regarding this equation. The first observation is that the property E, the energy of the control mass, was found to exist, and the first law for a change of state was written using Eq3. However, rather than deal with this property E, it is more convenient to consider the internal energy and the kinetic and potential energies of the mass.
The second observation is that Eq6 and Eq7 are in effect a statement of the conservation of energy. The net change of the energy of the control mass is always equal to the net transfer of energy across the boundary as heat and work. This is somewhat analogous to a joint checking account shared by a husband and wife. There are two ways in which deposits and withdrawals can be made—either by the husband or by the wife—and the balance will always reflect the net amount of the transaction. Similarly, there are two ways in which energy can cross the boundary of a control mass—either as heat or as work—and the energy of the mass will change by the exact amount of net energy crossing the boundary. The concept of energy and the law of conservation of energy are basic to thermodynamics.
The last observation is that Eq6 and Eq7 can give only changes in internal energy, kinetic energy, and potential energy. Nothing can be learned about absolute values of these quantities from these equations. If it is desired to assign values to internal energy, kinetic energy, and potential energy, reference states must be assumed and values must be assigned to the quantity in this reference state. The kinetic energy of a body with zero velocity relative to the earth is assumed to be zero. Similarly, the value of the potential energy is assumed to be zero when the body is at some reference elevation. With internal energy, therefore, a reference state must exist if it is desired to assign values of this property.
