Dimensionless Conduction Heat Rates

Cases 1 through 4 are associated with conduction from objects held at an isothermal temperature (T1) that are embedded within an infinite medium of uniform temperature (T2) at locations removed from the object. For the infinite medium cases, useful results may be obtained by defining a characteristic length:

Lc ≡ (
As
4π
)
1/2
 
 

where As is the surface area of the object. Conduction heat transfer rates from the object to the infinite medium may then be reported in terms of a dimensionless conduction heat rate:

q =
qss* kAs(T1 − T2)
Lc

From the table, it is evident that the values of qss*, which have been obtained analytically and numerically, are similar for a wide range of geometrical configurations. As a consequence of this similarity, values of qss* may be estimated for configurations that are similar to those for which qss* is known. For example, dimensionless conduction heat rates from cuboid shapes (case 4) over the range 0.1 ≤ d/w ≤ 10 may be closely approximated by interpolating the values of qss* reported in the table. Note that results for qss* in the table may be converted to expression for S in the reference Conduction Shape Factors. For example, the shape factor of Case 10 from the reference Conduction Shape Factors may be derived from the dimensionless conduction heat rate of Case 2 (recognizing that the infinite medium can be viewed as two adjacent semi-infinite media).

System Schematic Active Area, As qss*
Case 1
Isothermal sphere of diameter D and temperature T1 in an infinite medium of temperature T2		 πD 2 1
Case 2
Infinitely thin, isothermal disk of diameter D and temperature T1 in an infinite medium of temperature T2
πD 2
2
2√2
π
  = 0.900
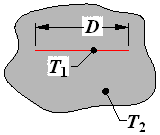Case 3
Infinitely thin rectangle of length L, width w, and temperature T1 in an infinite medium of temperature T2		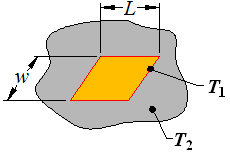 2wL 0.932
Case 4
Cuboid shape of height h with a square footprint of width w and temperature T1 in an infinite medium of temperature T2		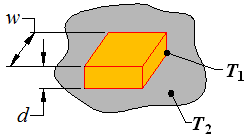 2w 2 + 4wd
d
w
qss*
0.10.943
1.00.956
2.00.961
101.111