Quick
Continuous deformation under load is called creep.
Equation
Nomenclature
Details
If stress is applied to a material at an elevated temperature, the material may stretch and eventually fail, even though the applied stress is less than the yield strength at that temperature. Plastic deformation at high temperatures is known as creep.
To determine the creep characteristics of a material, a constant stress is applied to a heated specimen in a creep test. As soon as the stress is applied, the specimen stretches elastically a small amount ε, depending on the applied stress and the modulus of elasticity of the material at the high temperature.
Dislocation Climb
High temperatures permit dislocations in a metal to climb. In climb, atoms move either to or from the dislocation line by diffusion, causing the dislocation to move in a direction that is perpendicular, not parallel, to the slip plane. The dislocation escapes from lattice imperfections, continues to slip, and causes additional deformation of the specimen even at low applied stresses.
Creep Rate and Rupture Times
During the creep test, strain or elongation is measured as a function of time and plotted to give the creep curve as shown:
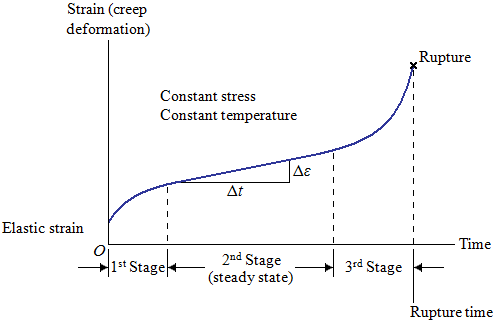
The curve exhibits three distinct regions. In the first stage of creep of metals, many dislocations climb away from obstacles, slip, and contribute to deformation. The first stage includes both elastic and plastic deformation. This stage shows a decreasing creep rate, which is due to strain hardening. Eventually, the rate at which dislocations climb away from obstacles equals the rate at which dislocations are blocked by other imperfections. This leads to second-stage, or steady-state, creep. The slope of the steady-state portion of the creep curve is the creep rate:
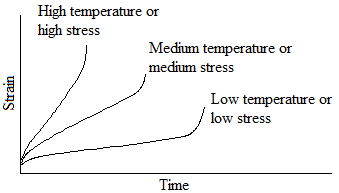
The second stage shows a constant minimum creep rate caused by the annealing effect. Eventually, during third-stage creep, necking begins (the specimen shows considerable reduction in area), the true stress increases, and the specimen deforms at an accelerated rate until failure (or fracture) occurs. The time required for failure to occur is the rupture time. Either a higher stress or a higher temperature reduces the rupture time and increases the creep rate as shown in the following figure:
The combined influence of applied stress and temperature on the creep rate and rupture time tr follows an Arrhenius relationship:
Creep rate = Cσ n exp (−Qc/RT)
and:
tr = Kσ m exp (Qm/RT)
where R is the gas constant, T is the temperature in Kelvin, C, K, n, and m are constants for the material. Qc is the activation energy for creep, and Qr is the activation energy for rupture. In particular, Qc is related to the activation energy for self-diffusion when dislocation climb is important.
In crystalline ceramics, other factors—including grain boundary sliding and nucleation of microcracks—are particularly important. Often, a noncrystalline or glassy material is present at the grain boundaries; the activation energy required for the glass to deform is low, leading to high creep rates compared with completely crystalline ceramics. For the same reason, creep occurs at a rapid rate in ceramic glasses and amorphous polymers.
The stress-dependent part of plastic deformation is referred to as slip, and the time-dependent part—which is also influenced by the temperature—as creep.

