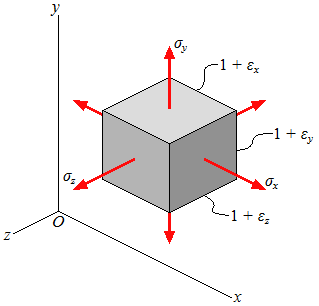
---

Multiaxial Loading and Generalized Hooke's Law

---

Equations

(Eq1)     εx = σx E  −  νσy E  −  νσz E	strain in x direction, generalized Hooke's law
(Eq2)     εy =  − νσx E  +  σy E  −  νσz E	strain in y direction, generalized Hooke's law
(Eq3)     εz =  − νσx E  −  νσy E  +  σz E	strain in z direction, generalized Hooke's law

Nomenclature

ε	strain
σ	stress
E	Young's modulus
ν	Poisson's ratio

Details

Consider a slender member subjected to an axial load. Choosing the axis along which the load is applied as the x axis, and denoting by P the internal force at a given location, the corresponding stress components are found to be σ_x = P/A and σ_y = σ_z = 0.

Now consider a structural element subjected to loads acting in the directions of the three coordinate axes and producing normal stresses σ_x, σ_y, and σ_z which are all different from zero. This condition is referred to as a multiaxial loading. Examine the following figure:



Note that this is not the general stress condition described in the lesson Stress Under General Loading Conditions and Components of Stress, since no shearing stresses are included among the stresses shown in the above figure.

Consider an element of an isotropic material in the shape of a cube as shown below left. Assume that each side of the cube is equal to unity, since it is always possible to select the side of the cube as a unit of length. Under the given multiaxial loading, the element will deform into a rectangular parallelepiped of sides equal, respectively, to 1 + ε_x, 1 + ε_y, and 1 + ε_z, where ε_x, ε_y, and ε_z denote the values of the normal strain in the directions of the three coordinate axes as shown in the figure at below right.

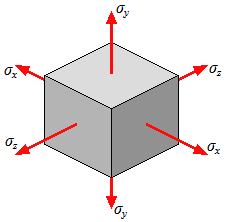
Unstressed	Stressed

It should be noted that, the element under consideration could also undergo a translation, but the only concern here is with the actual deformation of the element, and not with any possible superimposed rigid-body displacement.

In order to express the strain components ε_x, ε_y, and ε_z in terms of the stress components σ_x, σ_y, and σ_z, the effect of each stress component will be considered separately and the obtained results will be combined. The approach proposed here is based on the principle of superposition. This principle states that the effect of a given combined loading on a structure can be obtained by determining separately the effects of the various loads and combining the results obtained, provided that the following conditions are satisfied:

1. Each effect is linearly related to the load that produces it.
2. The deformation resulting from any given load is small and does not affect the conditions of application of the other loads.

In the case of multiaxial loading, the first conditions will be satisfied if the stresses do not exceed the proportional limit of the material, and the second condition will also be satisfied if the stress on any face does not cause deformations of the other faces that are large enough to affect the computation of the stresses on those faces.

Considering first the effect of the stress component σ_x, recall from the lesson Poisson's Ratio that σ_x causes a strain equal to σ_x/E in the x direction, and strains equal to −νσ_x/E in each of the y and z directions. Similarly, the stress component σ_y, if applied separately, will cause a strain σ_y/E in the y direction and strains −νσ_y/E in the other two directions. Finally, the stress component σ_z causes a strain σ_z/E in the z direction and strains −νσ_z/E in the x and y directions. Combining the results obtained, it may be concluded that the components of strain corresponding to the given multiaxial loading are:

(Eq1)

εx = σx E  −  νσy E  −  νσz E

(Eq2)

εy =  − νσx E  +  σy E  −  νσz E

(Eq3)

εz =  − νσx E  −  νσy E  +  σz E

The relations given by Eq1, Eq2, and Eq3 are referred to as the generalized Hooke's law for the multiaxial loading of a homogeneous isotropic material. As indicated earlier, the results obtained are valid only as long as the stresses do not exceed the proportional limit, and as long as the deformations involved remain small. Also recall that a positive value for a stress component signifies tension, and a negative value compression. Similarly, a positive value for a strain component indicates expansion in the corresponding direction, and a negative value contraction.