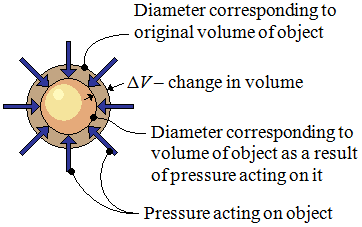
Fig1. A solid sphere subject to uniform bulk stress from a fluid.
| Bulk Stress |
| Bulk stress |
| B | bulk modulus |
| ΔV | absolute value of the change in volume of object |
| V | original volume of object |

Fig1. A solid sphere subject to uniform bulk stress from a fluid. |
| (Eq1) |
|
| (Eq1) |
|