| Bulk Modulus and Dilation |
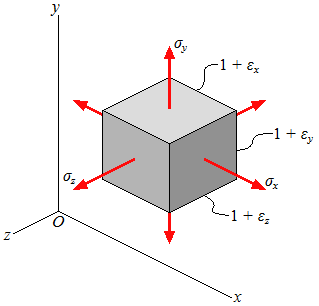
| Dilation, or change in volume per unit volume | |||||||
| Dilation, or change in volume per unit volume | |||||||
| Bulk modulus, or modulus of compression | |||||||
| Dilation, or change in volume per unit volume | |||||||
| Bulk modulus |
| e | dilation |
| k | bulk modulus (mechanics of materials) |
| B | bulk modulus (physics) |
| ε | strain |
| E | modulus of elasticity |
| σ | stress |
| p | pressure |
| ν | Poisson's ratio |
| V | volume |
| Δp | change in pressure |
| ΔV | change in volume |
| V0 | initial volume |
 |  |
| Unstressed | Stressed |
| (Eq1) |
|
| e = |
| − |
|
| (Eq2) |
|
| (Eq3) |
|
| (Eq4) |
|
| (Eq5) |
|
| (Eq6) |
|