---

Torque, Inertia, and Angular Acceleration for A Rigid Body

---

This lesson will represent the fundamental relation for the rotational dynamics of a rigid body. The angular acceleration of a rotating body is directly proportional to the sum of the torque components along the axis of rotation. The proportionality factor is the moment of inertia.

To develop the relation, imagine the body as being made up of a large number of particles. Choosing the axis of rotation to be the y-axis, the first particle has mass m₁ and distance r₁ from the axis. The net force acting on the particle has a component F_1,rad along the radial direction, a component F_1,tan that is tangent to the circle of radius r₁ in which the particle moves as the body rotates, and a component F_1y along the axis of rotation. Newton's second law for the tangential component is:

F_1,tan = m₁a_1,tan

The tangential acceleration can be expressed of the first particle in terms of the angular acceleration α, using the equation for the tangential acceleration of a point on a rotating body. This equation is:a_1,tan = r₁α. Using this relation and multiplying both sides of Eq1 by r₁, the following equation results:

F_1,tanr₁ = m₁r₁²α

From the
Quick

A force is a push or pull. It is a vector quantity. English units are pound-force, lb_f. Metric units are newton, N. Force is equal to mass multiplied by acceleration.


Details

The concept of force allows for a quantitative description of the interaction between two bodies or between a body and its environment. One that pushes on a car that is stuck in the snow, is exerting a force on the car. A locomotive exerts a force on the train cars it is pulling or pushing. A steel cable exerts a force on the beam it hoists at a construction site.

Contact forces include pushes or pulls exerted by a hand, the force of a rope pulling on a block to which it is tied, or the friction force that the ground exerts on a ball player sliding into home. There are also long-range forces, for example such as what are experienced between a pair of magnets. Gravity, too, is a long-range force — the sun exerts a gravitational pull on the earth, even over a distance of 150 million kilometers, that keeps the earth in orbit. The force of gravitational attraction that the earth exerts on your body is called your weight.

Force is a vector quantity; a body can be pushed or pulled in different directions. Thus to describe a force, the direction in which it acts as well as its magnitude need to be described. In this case, the magnitude describes "how much" or "how hard" the force pushes or pulls. The SI unit of the magnitude of force is the newton.

When two forces ₁ and ₂ act at the same time at point A of the body shown, the effect on the body's motion is the same as the effect of a single force 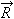equal to the vector sum of the original forces: 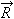= ₁ + ₂. More generally, the effect of any number of forces applied at a point on a body is the same as the effect of a single force equal to the vector sum of the forces. This important principle goes by the name superposition of forces.

The fact that forces may combine according to vector addition allows a force to be replaced by its component vectors, as with displacements. For example, in the following figure, force acts on a body at point O.



The component vectors of in the directions O_x and O_y are _x and _y. When _x and _y are applied simultaneously, as in the next figure, the effect is exactly the same as the effect of the original force .



Any force can be replaced by its component vectors, acting at the same point.

It is frequently more convenient to describe a force in terms of its x- and y-components F_x and F_y rather than by its component vectors. For the case of the above two pictures, both F_x and F_y are positive; for other orientations of the force , either F_x or F_y can be negative or zero.

There is no law that says our coordinate axes have to be vertical and horizontal.

Typically, a force is represented as either a push or a pull. A push is associated with compression and a push is associated with tension.

For a static body, the sum of all forces is equal to zero.

Sometimes a force is referred to as the load. Or when loading is mentioned, it is typically referring to force.

A force has both magnitude and direction; hence, it is a vector quantity. The magnitude is a scalar quantity that defines the strength of the force. The direction is represented by an arrow pointing in the direction that the force is acting.