EngArc - L - Vector Product (Cross Product)

Vector Product

Quick

V = P × Q
(read as v equals the vector product (or cross product) of p and q)
where V, P, and Q are vectors and the magnitude of V is:
V = PQ sin θ

Details

The vector product, also known as the cross product (because of the notation), is a vector (arbitrarily named vector C) that results from specific operations which take into consideration two other vectors (arbitrarily named vector A and vector B).

The general notation for the vector product of the two vectors A and B is written like this:

C = A × B

The sign × looks like a multiplication sign but it is a vector product sign.

The order that A and B are written is important, as A and B are not commutative, furthermore:

A × B = -(B × A)

Conditions which must be satisfied

The vector product (vector C) must be perpendicular to the plane that containins A and B.

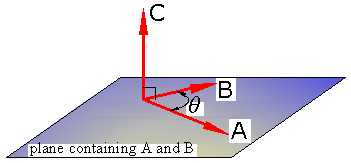
The magnitude of C must equal the product of the magnitudes of A and B and of the sine of the angle θ (must be 180° or less) formed by A and B:

(Eq1) C = AB sin θ
The direction of C is found by using the right-hand rule. The right-hand rule is used primarily in accordance with the vector product.

The vector (vector C) that satisfies these three conditions (which define it uniquely) is referred to as the vector product of A and B; it is represented by the mathematical expression C = A × B.

Right Hand Rule

An open fist is formed with the right hand. Using a motion that one would use to tighten an object, the fingers are curled in the same sense as the rotation through θ which brings the vector A in line with the vector B.

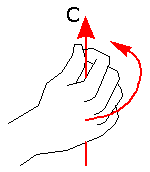
Note: This is only if the vector product A × B is being taken. If the vector product B × A is being taken, then the fingers are curled in the same sense as the rotation through θ which brings the vector B in line with the vector A, and the vector would then point in the opposite direction. The thumb points in the direction of the vector C. Note that if A and B do not originate from the same point, they should first be redrawn from the same point.

For C = A × B, the three vectors, A, B, and C - taken in that order - form a right-handed triad.

Further Explanation

When two vectors A and B have either the same direction or opposite directions, their vector product is zero (sin (0°) = sin (180°) = 0). In the general case when the angle θ formed by the two vectors is neither 0° nor 180°, Eq1 can be given a simple geometric interpretation: The magnitude C of the vector product of A and B is equal to the area of the parallelogram which has A and B for sides. Eq1 is in fact equal to the equation for the area of a parallelogram. The vector product A × B will therefore remain unchanged if B is replaced by a vector D which is coplanar with A and B and such that the line joining the tips of B and D is parallel to A.

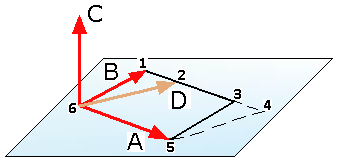
The corresponding equation is:

C = A × B = A × D

From the above picture, it can be seen that the area 1,3,5,6 is equal to the area 2,4,5,6.

Vector Product and the Distributive Property

The distributive property is valid with the vector product as represented in the following equation:

A × (B1 + B2) = A × B1 + A × B2

Since the entire structure of both vector algebra and statics depends upon the relation above, the derivation follows:

Without loss of generality, it may be assumed that P is directed along the y axis fig3.9. Denoting by Q the sum of Q1 and Q2, we drop perpendicuulars from the tips of Q, Q1, and Q2 onto the zx plane, defining in this way the vectors Q', Q'1, and Q'2. These vectors will be referred to, respectively, as the projections of Q, Q1, and Q2 on the zx plane. Recalling the property expressed by eq3.3, we note that the left-hand member of eq3.5 can be replaced by P X Q' and that, similarly, the vector products P X Q1 and P X Q2 can respectively be replaced by P X Q'1 and P X Q'2. Thus, the relation to be proved can be written in the form

P X Q' = P X Q'1 + P X Q'2

We now observe that P X Q' can be obtained from Q' by multiplying this vector by the scalar P and rotating it counterclockwise through 90° in the zx plane fig3.9b; the other two vector products in 3.5' can be obtained in the same manner from Q'1 and Q'2, respectively. Now, since the projection of a parallelogram onto an arbitrary plane is a parallelogram