
Figure 1
Reversible heat engine cycle.
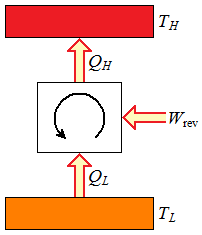
Figure 2
Reversible refrigeration cycle.
| Inequality of Clausius |
| Inequality of Clausius |
| Q | Heat |
| QH | Heat associated with high-temperature reservoir |
| QL | Heat associated with low-temperature reservoir |
| T | Temperature |
| TH | Temperature of high-temperature reservoir |
| TL | Temperature of low-temperature reservoir |
| Wrev | Reversible work |
| (Eq1) |
|
 Figure 1 Reversible heat engine cycle. |  Figure 2 Reversible refrigeration cycle. |
| ∮ | δQ = QH − QL < 0 |
| ∮ |
| = |
| − |
| = 0 |
| ∮ | δQ ≥ 0 |
| ∮ |
| = 0 |
| ∮ | δQ = QH − QL,irr > 0 |
| ∮ |
| = |
| − |
| < 0 |
| ∮ | δQ = 0 |
| ∮ |
| < 0 |
| ∮ | δQ ≥ 0 |
| ∮ |
| < 0 |
| ∮ | δQ = −QH + QL < 0 |
| ∮ |
| = − |
| + |
| = 0 |
| ∮ | δQ = 0 |
| ∮ |
| = 0 |
| ∮ | δQ ≤ 0 |
| ∮ |
| = 0 |
| ∮ | δQ = −QH,irr + QL < 0 |
| ∮ |
| = − |
| + |
| < 0 |
| ∮ | δQ < 0 |
| ∮ |
| < 0 |
| ∮ |
| = 0 |
| ∮ |
| < 0 |
| (Eq1) |
|