---

Capillary Effect

---

Equation

(Eq1)     h = 2σs ρgR cos φ        (R = constant)

capillary rise

Details

An interesting consequence of surface tension is the capillary effect, which is the rise or fall of a liquid in a small-diameter tube inserted into the liquid. The rise of kerosene through a cotton wick inserted into the reservoir of a kerosene lamp is due to this effect. The capillary effect is also partially responsible for the rise of water to the top of tall trees.

The strength of the capillary effect is quantified by the contact (or wetting) angle φ, defined as the angle that the tangent to the liquid surface makes with the solid surface at the point of contact. The surface tension force acts along this tangent line toward the solid surface. A liquid is said to wet the surface when φ < 90° and not to wet the surface when φ > 90°. In atmospheric air, the contact angle of water (and most other organic liquids) with glass is nearly zero, φ ≈ 0° as in the figure. Therefore, the surface tension force acts upward on water in a glass tube along the circumference, tending to pull the water up. As a result, water rises in the tube until the weight of the liquid in the tube above the liquid level of the reservoir balances the surface tension force. The contact angle is 130° for mercury—glass and 26° for kerosene—glass in air. Note that the contact angle, in general, is different in different environments (such as another gas or liquid in place of air).

The phenomenon of capillary effect can be explained microscopically by considering cohesive forces and adhesive forces. The liquid molecules at the solid—liquid interface are subjected to both cohesive forces by other liquid molecules and adhesive forces by the molecules of the solid. The relative magnitudes of these forces determine whether a liquid wets a solid surface or not. Obviously, the water molecules are more strongly attracted to the glass molecules than they are to other water molecules, and thus water tends to rise along the glass surface. The opposite occurs for mercury, which causes the liquid surface near the glass wall to be suppressed as shown. 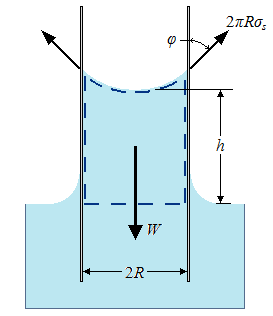The magnitude of the capillary rise in a circular tube can be determined from a force balance on the cylindrical liquid column of height h in the tube as shown in the figure. The bottom of the liquid column is at the same level as the free surface of the reservoir, and thus the pressure there must be atmospheric pressure. This balances the atmospheric pressure acting at the top surface, and thus these two effects cancel each other. The weight of the liquid column is approximately:

W = mg = ρVg = ρg(πR²h)

Equating the vertical component of the surface tension force to the weight gives:

W = F_surface → ρg(πR²h) = 2πRσ_scos φ

Solving for h gives the capillary rise to be:

(Eq1)

h = 2σs ρgR cos φ        (R = constant)

Where h is the capillary rise. This relation is also valid for nonwetting liquids (such as mercury in glass) and gives the capillary drop. In this case φ > 90° and thus cos φ < 0, which makes h negative. Therefore, a negative value of capillary rise corresponds to a capillary drop as shown.

Note that the capillary rise is inversely proportional to the radius of the tube. Therefore, the thinner the tube is, the greater the rise (or fall) of the liquid in the tube. In practice, the capillary effect is usually negligible in tubes whose diameter is greater than 1 cm. When pressure measurements are made using manometers and barometers, it is important to use sufficiently large tubes to minimize the capillary effect. The capillary rise is also inversely proportional to the density of the liquid, as expected. Therefore, lighter liquids experience greater capillary rises. Finally, it should be kept in mind that Eq1 is derived for constant-diameter tubes and should not be used for tubes of variable cross-section.