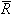
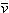
| Ideal Gas Equation |
| symbol | description |
| m | mass |
| M | molar mass |
| n | number of moles (in kmol) of gas |
| P | pressure |
| R | unique gas constant for each gas |
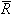 | universal gas constant |
| T | temperature |
| v | specific volume |
| V | volume |
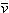 | ? |
| ρ | density |
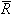 T
T
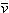 =
= 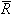 T
T
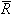 is the universal gas constant, the value of which is, for any gas, 8.3145 kJ/kmolK. Note that, as indicated by the nomenclature above, that
is the universal gas constant, the value of which is, for any gas, 8.3145 kJ/kmolK. Note that, as indicated by the nomenclature above, that 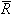 is different from R. R is a unique value, which is different for each gas.
is different from R. R is a unique value, which is different for each gas.
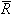 T
T
| R = |
|
| PV = |
| RT |
| ρ = |
|
| = |
| = constant |
| Boyle's law | Charles's law | Avogadro's law |
| V = constantB/P | V = (constantC )(T) | V = (constantA)(n) |
| with T and n held constant | with P and n held constant | with T and P held constant |
| V = a constant |
|
| R = |
| = |
| = 0.082058 |
|