---

Angles of Friction

---

Equations

tan φs = μs

tan φk = μk

Nomenclature

symbol	description
φs	angle of static friction
φk	angle of kinetic friction
μs	coefficient of static friction
μk	coefficient of kinetic friction
N	normal component of the reaction surface

Explanation

It is sometimes convenient to replace the normal force N and the friction force F by a resultant R. Consider a block of weight W resting on a horizontal plane surface:

No friction	R = N		If no horizontal force is applied to the block, the resultant R reduces to the normal force N.
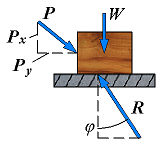
No motion	F = Px φ < φs		However, if the applied force P has a horizontal component Px which tends to move the block, the force R will have a horizonatal component F and, thus, will form an angle φ with the normal to the surface as shown.
Motion impending	Fm = Px φ = φs		If Px is increased until motion becomes impending, the angle between R and the vertical grows and reaches a maximum value.

This maximum value is called the angle of static friction and is denoted by φ_s. From the geometry of the previous figure, the equation is:

tan φs =

Fm N

=

μsN N

tan φs = μs

Motion

F = Px φ < φs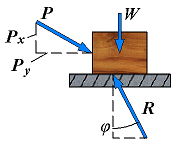

If motion actually takes place, the magnitudes of the friction force drops to Fk; similarly, the angle φ between R and N drops to a lower value φk, called the angle of kinetic friction.

From the geometry of the previous figure, the equation is:

tan φk =

Fk N

=

μkN N

tan φk = μk

Another example may show how the angle of friction can be used to advantage in the analysis of certain types of problems. Consider a block resting on a base and subjected to no other force than its weight W and the reaction R of the board. The board can be given any desired inclination.

No friction	R = N		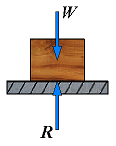If the base is horizontal, the force R exerted by the board on the block is perpendicular to the base and balances the weight W.
No motion	F = Px φ < φs		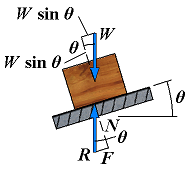If the base is given a small angle of inclination, θ, the force R will deviate from the perpendicular to the base by the angle θ and will keep balancing W; it will then have a normal componenet N of magnitude N = W cos θ and a tangential component F of magnitude F = W sin θ.
Motion impending	Fm = Px φ = φs		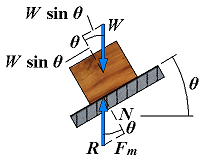If the angle of inclination continues to increase, motion will soon become impending. At that time, the angle between R and the normal will have reached its maximum value φs. The value of the angle of inclination corresponding to impending motion is called the angle of repose. Clearly, the angle of repose is equal to the angle of static friction φ.
Motion impending	Fm = Px φ = φs		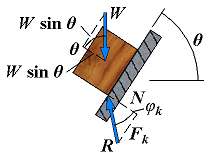If the angle of inclination θ is further increased, motion starts and the angle between R and the normal drops to the lower value φk. The reaction R is not vertical any more, and the forces acting on the block are unbalanced.

---

⇐Previous Lesson: Laws of Dry Friction and Coefficients of Friction

Next Lesson: Encountering Dry Friction⇒