The block mass is 8 kg, the film contact area (A) is 50 cm2, θ = 20°, the fluid film thickness (h) is 0.85-mm, and the fluid is SAE 30 oil at 20°C
Find
The terminal velocity of the block.
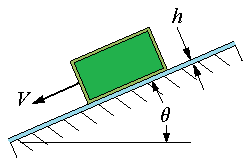
| Terminal Velocity of an Inclined Block on a Fluid |
|
Conditions
The block mass is 8 kg, the film contact area (A) is 50 cm2, θ = 20°, the fluid film thickness (h) is 0.85-mm, and the fluid is SAE 30 oil at 20°C Find The terminal velocity of the block. |  |
| τ = μ |
|
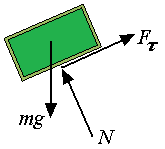
| μ |
| A = mg sin θ |
| umax = |
|
| umax = |
|