Quick
Enthalpy is a combination of the properties of internal energy plus pressure times volume. It is a point function and an extensive property.
Equations
|
|
enthalpy
|
|
|
specific enthalpy
|
Nomenclature
Details
Through the analysis of specific types of processes, certain combinations of thermodynamic properties are frequently encountered. Certain combinations of properties can be lumped together into a single property, which is therefore also a property of the substance undergoing the change of state. Enthalpy is one of these properties. For example, consider a control mass undergoing a quasi-equilibrium isobaric process, as shown:
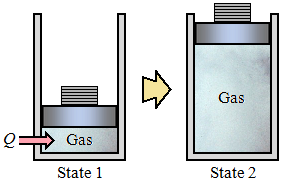
Assume that there are no changes in kinetic or potential energy and that the only work done during the process is that associated with the boundary movement. Taking the gas as the control mass and applying the first law, the following is obtained, in terms of Q:
1Q 2 = U2 − U1 + 1W 2
The work done can be calculated from the relation:
Since the pressure is constant:
| 1W 2 = | ∫ | | P dV = P(V2 − V1) |
Therefore:
1Q 2 = U2 − U1 + P2V2 − P1V1 = (U + PV)2 − (U + PV)1
It is found that, in this very restricted case, the heat transfer during the process is given in terms of the change in the quantity U + PV between the initial and final states. Because all these quantities are thermodynamic properties, that is, functions only of the state of the system, their combination must also have these same characteristics. Therefore, a new extensive property is defined, the enthalpy:
or, per unit mass, the specific enthalpy is:
As for internal energy, specific enthalpy h and total enthalpy H could be spoken of.
The heat transfer in a constant-pressure quasi-equilibrium process is equal to the change in enthalpy, which includes both the change in internal energy and the work for this particular process. This is by no means a general result. It is valid for this special case only because the work done during the process is equal to the difference in the PV product for the final and initial states. This would not be true if the pressure had not remained constant during the process.
The significance and use of enthalpy is not restricted to the special process just described. Many tables and charts of thermodynamic properties give values for enthalpy but not for internal energy. Therefore, it is necessary to calculate the internal energy at a state using the tabulated values and Eq2:
u ≡ h − Pv
Some may become confused about the validity of this calculation when analyzing system processes that do not occur at constant pressure, for which enthalpy has no physical significance. It must be kept in mind that enthalpy, being a property, is a state or point function, and its use in calculating internal energy at the same state is not related to, or dependent on, any process that may be taking place.
Tabular values of internal energy and enthalpy are all relative to some arbitrarily selected base. Because reference states are arbitrarily selected, it is always possible to have negative values for enthalpy. When enthalpy and internal energy are given values relative to the same reference state, as they are in essentially all thermodynamic tables, the difference between internal energy and enthalpy at the reference state is equal to Pv. Since the specific volume of the liquid is very small, this product is negligible as far as the significant figures of the tables are concerned, but the principle should be kept in mind, for in certain cases it is significant.
The enthalpy of a substance in a saturation state and with a given quality is found in the same way as the specific volume and internal energy. The enthalpy of saturated liquid has the symbol hf, saturated vapor hg, and the increase in enthalpy during vaporization hfg. For a saturation state, the enthalpy can be calculated by one of the following relations:
h = (1 − x)hfg + xhg
h = hf + xhfg
For substances for which compressed-liquid tables are not available, the enthalpy is taken as that of saturated liquid at the same temperature.
Like changes studied in a coffee-cup calorimeter, most changes in laboratories and manufacturing plants take place under the constant (approximately) pressure of Earth's atmosphere. Most biological reactions also take place under atmospheric pressure. The thermal energy gained or lost when a change takes place under constant pressure is called the enthalpy change ΔH. The symbol ΔH represents the difference between the final and initial enthalpies:
ΔH = Hfinal − Hinitial
The enthalpy of fusion (heat of fusion) is symbolized by ΔHfus and the enthalpy of vaporization (heat of vaporization) by ΔHvap. The enthalpy of neutralization is represented by ΔHneut. In general, ΔHreaction, ΔHrxn, or simply ΔH, stands for the enthalpy change accompanying a chemical reaction.
Stoichiometry
For many reactions, the thermal energy released is the chief reason for carrying out the reaction. For example, when natural gas is burned in a furnace or water heater, thermal energy is the desired product. When gasoline is burned in a car's engine, the thermal energy given off is converted to mechanical energy that moves the car. In an electric power plant, the thermal energy released by burning coal is converted to electrical energy.
Thermal energy given off can be shown as a product of the reaction in a thermochemical equation, for example:
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l) + 890.32 kJ
Thermochemical equations are always interpreted in terms of moles. Thermal energy absorbed can be shown as a reactant. More commonly, ΔHrxn is given to the right of the equation for a reaction:
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l) ΔHrxn = −890.32 kJ
The − sign for ΔHrxn shows that the reaction is exothermic. Thermal energy is lost by the system to the surroundings. When ΔHrxn is given for a reaction, the equation for the reaction must be interpreted in terms of moles (the number of moles shown in the equation).
