Quick
An irreversible process is a process that cannot return a system to its original conditions without leaving a change in its surroundings.
Details
The system and the surroundings would not return to their original conditions if the process was reversed. For example, an automobile engine does not give back the fuel it took to drive up a hill as it coasts back down the hill. There are many factors that make a process irreversible. Four of the most common causes of irreversibility are friction, unrestrained expansion of a fluid, heat transfer through a finite temperature difference, and mixing of two different substances. These factors are present in real, irreversible
processes and prevent these processes from being reversible.
Example
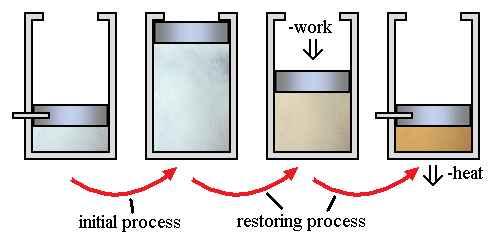
A gas is contained in a cylinder fitted with a piston. Consider the figure below, in which a gas, which is defined as the system, is restrained at high pressure by a piston that is secured by a pin. When the pin is removed, the piston is raised and forced abruptly against the stops. Some work is done by the system, since the piston has been raised a certain amount. A way to restore the system to its initial state would be to exert a force on the piston and thus compress the gas until the pin can be reinserted in the piston. Since the pressure on the face of the piston is greater on the return stroke than on the initial stroke, the work done on the gas in this reverse process is greater than the work done by the gas in the initial process. An amount of heat must be transferred from the gas during the reverse stroke so that the system has the same internal energy as it had originally. Thus, the system is restored to its initial state, but the surroundings have changed by virtue of the fact that work was required to force the piston down and heat was transferred to the surroundings. The initial process therefore is an irreversible one because it could not be reversed without leaving a change in the surroundings.
Factors that Contribute to Irreversibility
Friction
It is readily evident that friction makes a process irreversible. Consider a block and inclined plane which make up a system. The block is pulled up the inclined plane by weights at the other end. A certain amount of work is required for this to happen. Some of the work required is used to overcome the friction between the block and the plane, and some is used to increase the potential energy of the block. The block can be restored to its initial position by removing some of the weights and thus allowing the block to slide back down the plane. Some heat transfer from the surroundings will be required to restore the block to its initial temperature. Friction has rendered the process irreversible because the surroundings are not restored to their initial state at the conclusion of the reverse process.
Unrestrained Expansion
The classic example of an unrestrained expansion, as shown in the following figure, is a gas separated from a vacuum by a membrane. Consider what happens when the membrane breaks and the gas fills the entire vessel. It can be shown that this is an irreversible process by considering what would be necessary to restore the system to its original state. The gas would have to be compressed and heat transferred from the gas until its initial state is reached. Since the work and heat transfer involve a change in the surroundings, the surroundings are not restored to their initial state, indicating that the unrestrained expansion was an irreversible process.
In the reversible expansion of a gas, there must be only an infinitesimal difference between the force exerted by the gas and the restraining force, so that the rate at which the boundary moves will be infinitesimal. In accordance with the previous definition, this is a quasi-equilibrium process. However, actual systems have a finite difference in forces, which causes a finite rate of movement of the boundary, and thus the processes are irreversible in some degree.
Heat Transfer through a Finite Temperature Difference
Consider as a system a high-temperature body and a low-temperature body, and let heat be transferred from the high-temperature body to the low-temperature body. The only way in which the system can be restored to its initial state is to provide refrigeration, which requires work from the surroundings, and some heat transfer to the surroundings. Because of the heat transfer and the work, the surroundings are not restored to their original state, indicating that the process is irreversible.
An interesting question is now posed. Heat is defined as energy that is transferred through a temperature difference. It has just been shown that heat transfer through a temperature difference is an irreversible process. Therefore, how can a reversible process be attained? A heat-transfer process approaches a reversible process as the temperature difference between the two bodies approaches zero. Therefore, a reversible heat-transfer process is defined as one in which the heat is transferred through an infinitesimal temperature difference. But of course, to transfer a finite amount of heat through an infinitesimal temperature difference would require an infinite amount of time or infinite area. Therefore, all actual heat transfers are through a finite temperature difference and hence are irreversible, with the greater the temperature difference, the greater the irreversibility. However, the concept of reversible heat transfer is very useful in describing ideal processes.
Mixing of Two Different Substances
The figure below shows the process of mixing two different gases separated by a membrane. When the membrane is broken, a homogeneous mixture of oxygen and nitrogen fills the entire volume. This may be considered a special case of an unrestrained expansion, for each gas undergoes an unrestrained expansion as it fills the entire volume. A certain amount of work is necessary to separate the gases. Thus, an air separation plant requires an input of work to accomplish the separation.
Other Factors
A number of other factors make processes irreversible. Hysteresis effects and the i2R loss encountered in electrical circuits are both factors that make processes irreversible. Ordinary combustion is also an irreversible process.
It is frequently advantageous to distinguish between internal and external irreversibility. The following figure shows two identical systems to which heat is transferred. Assuming each system to be a pure substance, the temperature remains constant during the heat-transfer process. In one system the heat is transferred from a reservoir at a temperature T + dT, and in the other the reservoir is at a much higher temperature, T + ΔT, than the system. The first is a reversible heat-transfer process, and the second is an irreversible heat-transfer process. However, as far as the system itself is concerned, it passes through exactly the same states in both processes, which are assumed reversible. Thus, it can be said for the second system that the process is internally reversible but externally irreversible because the irreversibility occurs outside the system.
In a reversible process, the deviation from equilibrium is infinitesimal, and therefore it occurs at an infinitesimal rate. Since it is desirable that actual processes proceed at a finite rate, the deviation from equilibrium must be finite, and therefore the actual process is irreversible in some degree. The greater the deviation from equilibrium, the greater the irreversibility, and the more rapidly the process will occur.
Next Lesson: Reversible Process ⇒
Related
▪ L - Laws of Dry Friction and Coefficients of Friction
