What is it about a force that determines how effective it is in causing or changing rotational motion? The magnitude and direction of the force are important, but so is the position of the point where the force is applied. When you try to swing a heavy door open, it's a lot more effective to push farther away from the axis of rotation (near the knob) than close to the axis (near the hinges). In the figure, a wrench is being used to loosen a tight bolt. Force 
F |
b, applied near the end of the handle, is more effective than an equal force 
F |
a applied near the bolt. Force 
F |
c doesn't do any good at all; it's applied at the same point and has the same magnitude as 
F |
b, but it's directed along the length of the handle.
The quantitative measure of the tendency of a force to cause or change the rotational motion of a body is called torque. The figure shows a body that can rotate about an axis that passes through point O and is perpendicular to the plane of the figure. The body is acted on by three forces, 
F |
1, 
F |
2, and 
F |
3, in the plane of the figure. The tendency of 
F |
1 to cause a rotation about point O depends on its magnitude F1. It also depends on the perpendicular distance L1 between the line of action of the force (that is, the line along which the force vector lies) and point O. The distance L1 is called the lever arm (or moment arm) of force 
F |
1 about O. The twisting effort is directly proportional to both F1 and L1. The torque (or moment) is defined of the force 
F |
1 with respect to point O as the product F1L1. For a force of magnitude F whose line of action is a perpendicular distance L from the point O, the torque is:
τ = FL
Physicists usually use the term "torque", while engineers usually use the term "moment" (unless they are talking about a rotating shaft). Both groups use the term "lever arm" or "moment arm" for the distance L.
The lever are of 
F |
1 in the figure is the perpendicular distance OA or L1, and the lever arm of 
F |
2 is the perpendicular distance OB or L2. The line of action of 
F |
3 passes through the reference point O, so the lever arm for 
F |
3 is zero and its torque with respect to point O is zero. In the same way, force 
F |
c in the figure has zero torque with respect to point O. On the other hand, 
F |
b has a greater torque than 
F |
a because its lever arm is greater.
Note that torque is always defined with reference to a specific point, often (but not always) the origin of a coordinate system. If the position of this point is shifted, the torque of each force may also change. For example, the torque of force 
F |
3 in the figure is zero with respect to point O, but is not zero about point A or B. When describing the torque of a certain force, it's not enough to call it "the torque of 
F |
"; it must be said "the torque of 
F |
with respect to point X" or "the torque of 
F |
about point X."
Force 
F |
1 in the figure tends to cause counterclockwise rotation about O,
τ = rF
τ = rFsinθ
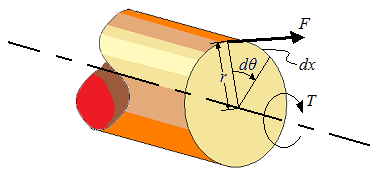
Torque and moment are both represented by the same units, or force multiplied by distance. Typically, in engineering, torque is with respect to rotational shafts, and moment is with respect to lever arms. In physics, the term torque may be used for both rotational shafts and lever arms.
Torque is commonly present with the use of shafts. Also, torque occurs when there is a force applied about a lever, where the lever experiences rotation, such as a wrench turning a nut.
What is torque exactly? Torque is the force applied times the shortest distance from the point of application of the force to the axis of the shaft. The distance is perpendicular to the axis of the shaft.
Related
▪ L - Torque in Relation to Work and Power
▪ L - Torque, Inertia, and Angular Acceleration for A Rigid Body
▪ L - Moment























